①若"小明得金牌"时，小华一定"不得金牌"，这与"王老师只猜对了一个"相矛盾，不合题意。
②若小明得银牌时，再以小华得奖情况分别讨论.如果小华得金牌，小强得铜牌，那么王老师没有猜对一个，不合题意；如果小华得铜牌，小强得金牌，那么王老师猜对了两个，也不合题意.
③若小明得铜牌时，仍以小华得奖情况分别讨论.如果小华得金牌，小强得银牌，那么王老师只猜对小强得奖牌的名次，符合题意；如果小华得银牌，小强得金牌，那么王老师猜对了两个，不合题意。
综上所述，小明、小华、小强分别获铜牌、金牌、银牌符合题意。
在1到2008（含2008）的所有正整数中，它的数码和可被5整除的数共有多少个？
2019-01-08 11:53:59
【解析】把0-1999中的个位去掉，得到从0-199中的一个数a，各位数字和除以5的余数为0、1、2、3、4中的一种，之后添加个位数字使新生成的数的各位数字之和能够整除5。不论a的各位数
把123，124，125三个数分别写在下图所示的A，B，C三个小圆圈中，然后按下面的规则修改这三个数。第一步，把B中的数改成A中的数与B中的数之和；第二步，把C中的数改成B中(已改过)的数与C中的数之
2019-01-08 09:11:04
当124在A中时，每次运算后的状态分别为：偶奇奇—偶奇奇—偶奇偶—偶奇偶—偶奇偶—偶奇奇—偶奇奇，需6步完成操作。当124在B中时，第一次后，B中的数字为偶数+奇数=奇数，而A、C也是奇
把一张无穷大的方格纸的每个结点都涂上4种颜色之一，使得每个方格的4个顶点的颜色都互不相同.求证方格纸上存在一条网格线，其上的结点只有两种不同颜色.
2019-01-08 08:30:26
【答案与解析】 考察一条水平网格线l上的结点涂色情况.如果任意相邻3个结点都只有两种颜色，则l上的所有结点也只有两种颜色，从而直线l即为所求.如果l上3个相邻点的颜色互不相
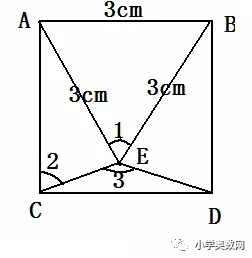下面是一个正方形，求出图中三个未知角的度数
2019-01-07 14:50:05
解：∠1在等边三角形ABE中，所以∠1=60度所以：∠BAE=60度，∠EAC=90-60=30（度）又因为：三角形EAC是等腰三角形（AC=AE=3）所以：∠2=（180-30）÷2=75（度）所以∠ECD=15（度）又因为这个图形是轴对阵图形
