答案解析：
这道题难在蚂蚁爬行的方向不断地发生变化，那么如果这两只蚂蚁都不调头爬行，相遇时它们已经爬行了多长时间呢？
非常简单，由于半圆周长为：1.26÷2=0.63米=63厘米，所以可列式为：1.26÷2÷（5.5+3.5）=7（秒）；我们发现蚂蚁爬行方向的变化是有规律可循的，它们每爬行1秒、3秒、5秒、…（连续的奇数）就调头爬行。
每只蚂蚁先向前爬1秒，然后调头爬3秒，再调头爬5秒，这时相当于在向前爬1秒的基础上又向前爬行了2秒；同理，接着向后爬7秒，再向前爬9秒，再向后爬11秒，再向前爬13秒，这就相当于一共向前爬行了1+2+2+2=7（秒），正好相遇。
解：
它们相遇时应是行了半个圆周，半个圆周长为：
1.26÷2=0.63（米）=63（厘米）；
如不调头，它们相遇时间为：
63÷（3.5+5.5）=7（秒）；
根据它们调头再返回的规律可知：
由于1-3+5-7+9-11+13=7（秒），
所以13+11+9+7+5+3+1=49（秒）相遇．
答：它们相遇时已爬行的时间是49秒。
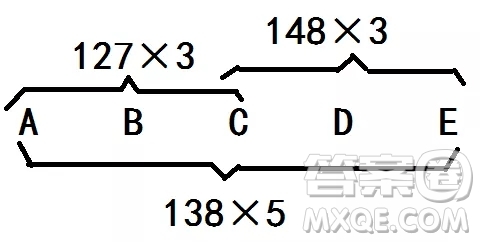有5个数，其平均数为138，按从小到大排列，从小到大数，前三个数的平均数为127，从大到小数，后三个数的平均数是148，则第三个数是多少？
2019-07-15 17:05:20
解析：如上图，求第三个数就是求C。5个数的平均数是138，能求出5个数的和是138×5=690，前三个数的和是127×3=381，后三个数的平均数是148×3=444，前三个数的和(A+B+C)+后三个数的和(C
甲、乙、丙、丁四人今年分别是16、12、11、9岁。问：多少年前，甲、乙的年龄和是丙、丁年龄和的2倍？
2019-07-15 16:46:55
答案与解析：解：这是一道年龄问题，也可以用方程来解决。等量关系为：多少年前，甲、乙的年龄和是丙、丁年龄和的2倍。关键：在相同的时间内，每个人增加或减少的年龄是相同的。设x年前，甲
在一条笔直的高速公路上，前面一辆汽车以每小时90千米的速度行驶，后面一辆汽车以每小时108千米的速度行驶．后面的汽车突然失控，向前冲去（车速不变）．在它鸣笛示警后5秒钟撞上了前面的汽车．在这辆车鸣笛时
2019-07-14 11:55:19
解：两车速度分别是：90千米/小时=25米/秒，108千米/小时=30米/秒，（30-25）×5，=5×5，=25（米），答：在这辆车鸣笛时两车相距25米．
n个自然数，它们的和乘以它们的平均数后得到2008。请问：n最小是多少？
2019-07-14 09:10:12
【答案】502。【解析】设这n个自然数的和为S，则它们的平均数为S÷n，依据题意得：S× （S÷n）= 2008则 S×S=2008×n=2×2×2×251×n等号的左边为一个完全平方数，那么等号右边n至少
