
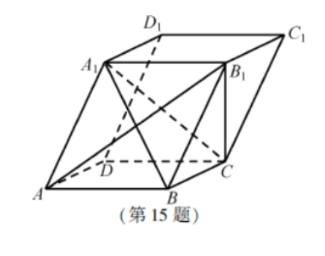
在平行六面体ABCD—A1B1C1D1中,AA1=AB,AB1⊥B1C1求证(1)AB//平面A1B1C;(2)平面ABB1A1⊥平面A1BC
本小题主要考查直线与直线、直线与平面以及平面与平面的位置关系,考查空间想能力和推理论证能力.满分14分
证明:
(1)在平行六面体 ABCD-A1B1C1D1中,AB∥A1B
因为AB¢平面A1B1C,A1B1c平面A1B1C
所以AB∥平面A1BC
(2)在平行六面体ABcD-A1B1C1D1中,四边形ABB1A1为平行四边形又因为AA1=AB,所以四边形ABB1A1为菱形
因此AB1⊥A1B
又因为AB1⊥B1C1,BC∥B1C1
所以AB1⊥BC
又因为A1B∩BC=B,AB平面A1BC,Bcc平面AtB
所以AB1⊥平面A1BC.
因为AB1c平面ABB1A1
所以平面ABB1A1⊥平面A1BC
已知,如图锐角三角形ABC内接于O,∠ABC=45°,点D是圆O上一点,过点D的切线DE交AC的延 且DE平行于BC,连接AD,BD,BE,AD的垂线AF与DC的延长线交于点F,求证△ABD相似于△ADE证明:
如图,在直角三角形ABC中,∠ACB=90°,CA=4.点P是半圆弧AC的中点,连接BP,线段BP把图形APCB分成两部分,则这两部分面积之差的绝对值是__解答:如图,设 AC 与 BP 相交于点 D,点 D 关于圆心 O
已知△ABC为锐角三角形,⊙O经过点 B,C,且与边AB,AC分别相交于点D,E. 若⊙O的半径与△ADE的外接圆的半径相等,则⊙O一定经过△ABC的()。解答:如图,连接BE.∵△ABC为锐角三角形,∴∠BAC,∠AB
口袋中有20个球,其中白球9个,红球5个,黑球6个.现从中任取10个球,使得白球不少于2个但不多于8个,红球不少于2个,黑球不多于3个,那么上述取法的种数是()。解答:用枚举法:红球 个数 白球 个