甲乙两人轮流往一个圆桌面上放同样大小的硬币。规则是：每人每次只能放一枚，硬币不许重叠，谁放完最后一枚硬币而使对方再也无处可放，谁就获胜。如果甲先放，那么他怎样放才能取胜？

g4b答案圈

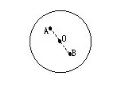
这道题初看太抽象，既不知道圆桌的大小，又不知道硬币的大小，谁知道该怎样放呀！我们用对称的思想来分析一下。圆是关于圆心对称的图形，若A是圆内除圆心外的任意一点，则圆内一定有一点B与A关于圆心对称（见右图，其中AO=OB）。g4b答案圈

所以，圆内除圆心外，任意一点都有一个（关于圆心的）对称点。由此可以想到，只要甲把第一枚硬币放在圆桌面的圆心处，以后无论乙将硬币放在何处，甲一定能找到与之对称的点放置硬币。也就是说，只要乙能放，甲就一定能放。最后无处可放硬币的必是乙。g4b答案圈

甲的获胜策略是：把第一枚硬币放到圆桌面的圆心处，以后总在乙上次放的硬币的对称点放置硬币。g4b答案圈

这种利用对称思想的获胜策略体现出了一种机智，而这种机智来源于数学思想。同学们经常进行这种锻炼，就会变得越来越聪明。比如，有两堆火柴，第一堆20根，第二堆25根，甲、乙二人轮流从中取火柴，每次可以从任一堆中取走任意数量的火柴，取走最后一根火柴者胜。甲先取，怎样才能保证获胜？利用对称的思想分析，只要甲先从第二堆中取走5根，此时两堆火柴的数量相等（也是一种对称），以后无论乙从哪一堆取多少根火柴，甲都对称地从另一堆取相同数量的火柴，只要乙能取，甲就能取，所以最后一根必被甲取走，甲胜。g4b答案圈